2022이전/알고리즘(하루에하나씩!)
Spanning Tree
바로퇴장
2020. 5. 24. 11:48
Spanning Tree란?
그래프 내의 모든 정점을 포함하느 트리
- Spanning Tree = 신장 트리 = 스패닝 트리
- Spanning Tree는 그래프의 최소 연결 부분 그래프이다.
- 최소연결 : 간선의 수가 적다.
- n의 정점을 가지는 그래프의 최소 간선의 수는 (n-1)개이고, (n-1)개의 간선으로 연결되어 있으면 필연적으로 트리 형태가 되고 이것이 바로 Spanning Tree가 된다.
Spanning Tree의 특징
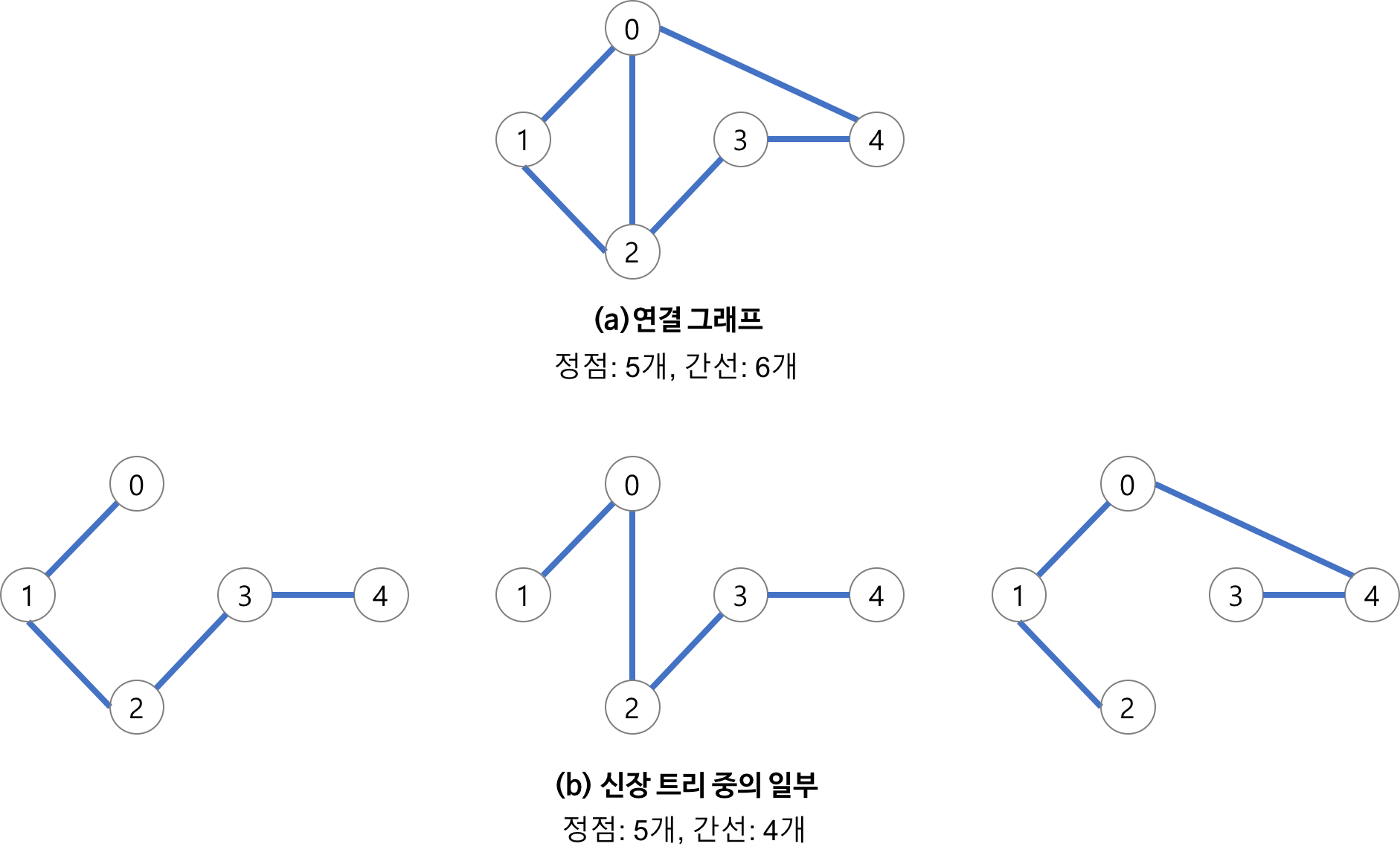
- DFS, BFS을 이용하여 그래프에서 신장 트리를 찾을 수 있다.
- 하나의 그래프에는 하나 이상의 신장 트리가 존재 할 수 있다.
- Spanning Tree는 트리의 특수한 형태이므로 모든 정점들이 연결 되어 있어야 하고 사이클을 포함해서는 안된다.
- 즉 Spanning Tree는 그래프에 있는 n개의 정점을 정확히 (n-1)개의 간선으로 연결 한다.
MST란?
Spanning Tree 중에서 사용된 간선들의 가중치 합이 최소인 트리
- MST = Minimum Spanning Tree = 최소 신장 트리
- MST는 간선에 가중치를 고려하여 최소 비용의 Spanning Tree를 선택하는 것을 말한다.
- 네트워크에 있는 모든 정점들을 가장 적은 수의 간선과 비용으로 연결하는 것이다.
MST의 특징
- 간선의 가중치의 합이 최소여야 한다.
- Spanning 특징을 모두 성립해야 한다.(간선의 갯수: n-1, 사이클x)
MST의 구현 방법
1. Kruskal MST 알고리즘
탐욕적인 방법(Greedy Algorithm)을 이용하여 네트워크의 모든 정점을 최비용으로 연결하는 최적 해답을 구하는 것
[과정]
- 그래프의 간선들을 가중치의 오름차순으로 정렬한다.
- 정렬된 간선 리스트에서 순서대로 사이클을 형성하지 않는 간선을 선택한다.(가장 낮은 가중치 먼저 선택, 사이클형성 간선 제외)
- 해당 간선을 현재의 MST(최소 비용 신장 트리)의 집합에 추가한다.








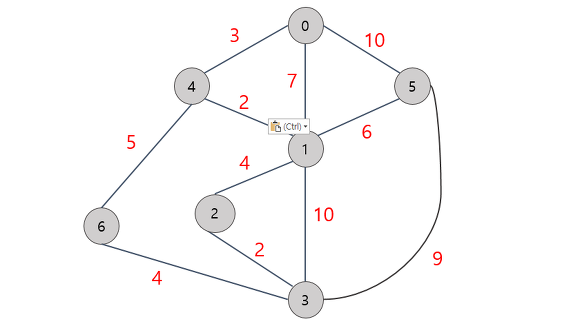
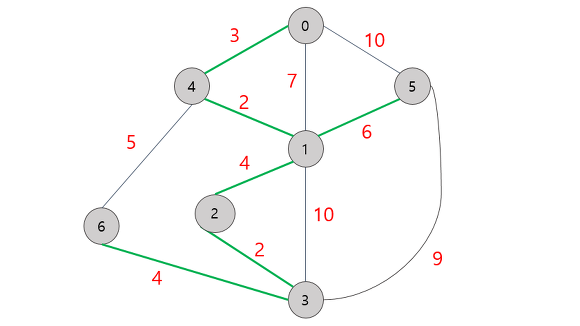
2. Prim MST 알고리즘
시작 정점에서부터 출발하여 신장트리 집합을 단계적으로 확장 해나가는 방법
- 정점 선택을 기반으로 하는 알고리즘이다.
- 이전 단계에서 만들어진 신장 트리를 확장하는 방법이다.
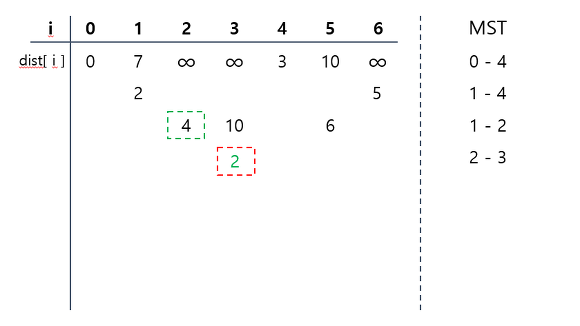
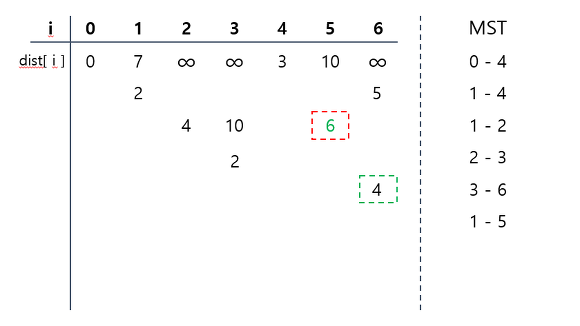
[과정]
- 시작 단계에서는 시작 정점만이 MST(최소 비용 신장 트리) 집합에 포함된다.
- 앞 단계에서 만들어진 MST 집합에 인접한 정점들 중에서 최소 간선으로 연결된 정점을 선택하여 트리를 확장한다.
- 위의 과정을 트리가 (N-1)개의 간선을 가질 때까지 반복한다.